We have a new paper proposing a simple model of reconfigurable robotics called Turning Machines, published at DNA26.

A Turning Machines lives on the hex grid in 2D, although it would also be easy to generalise the model to 3D. Here is an example Turning Machine trajectory folding a line into a Gosper curve:

Videos by Irina Kostitsyna

Why Turning Machines? Building molecular robots is hard; for example, the (more complicated) nubot model integrates rigid-body movement, self-assembly and finite state computational/logical control all in one system. This leads to an expressive model, but one that is challenging to implement in its fullest form. So to simplify things, in the Turning Machine model we have movement, but no self-assembly and extremely limited finite state control. The idea is to push the difficulty of molecular robotics away from wet-lab engineering and towards the theorists' brains. Luckily, despite the presence of the damp sluggish mass between my ears, my co-authors Cai and Irina supplied some big brains!

The paper begins by defining the model, an initial instance (input) of which is a horizontal line of monomers, each with a natural number state.

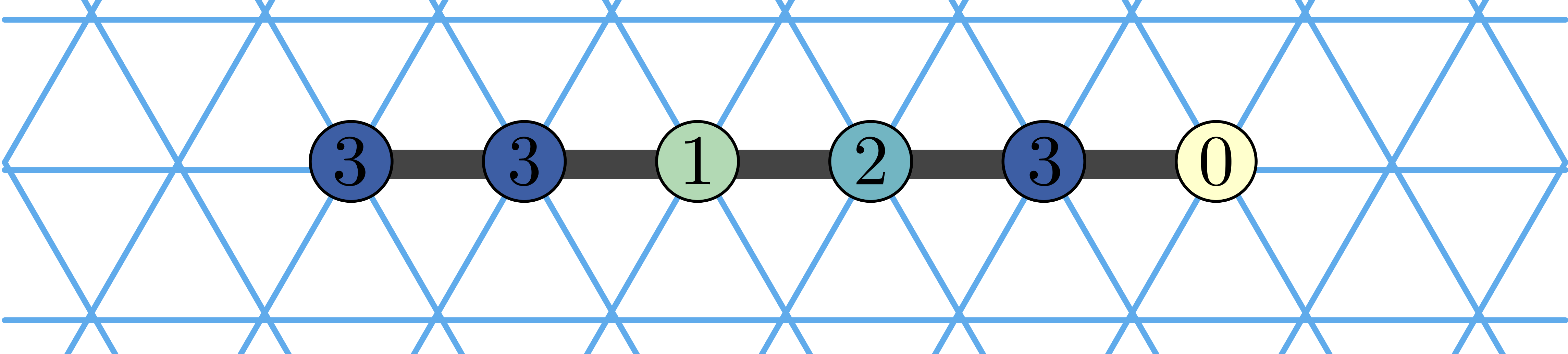
At each step, a monomer decrements its state and turns anti-clockwise, dragging other monomers with it, like this:

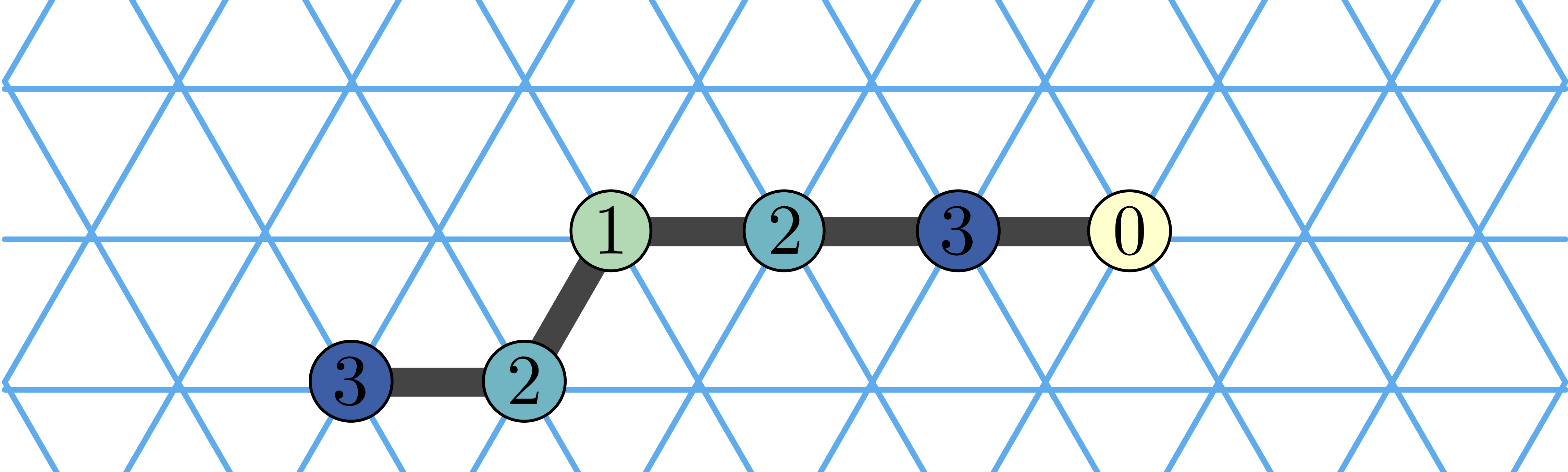
and then this:

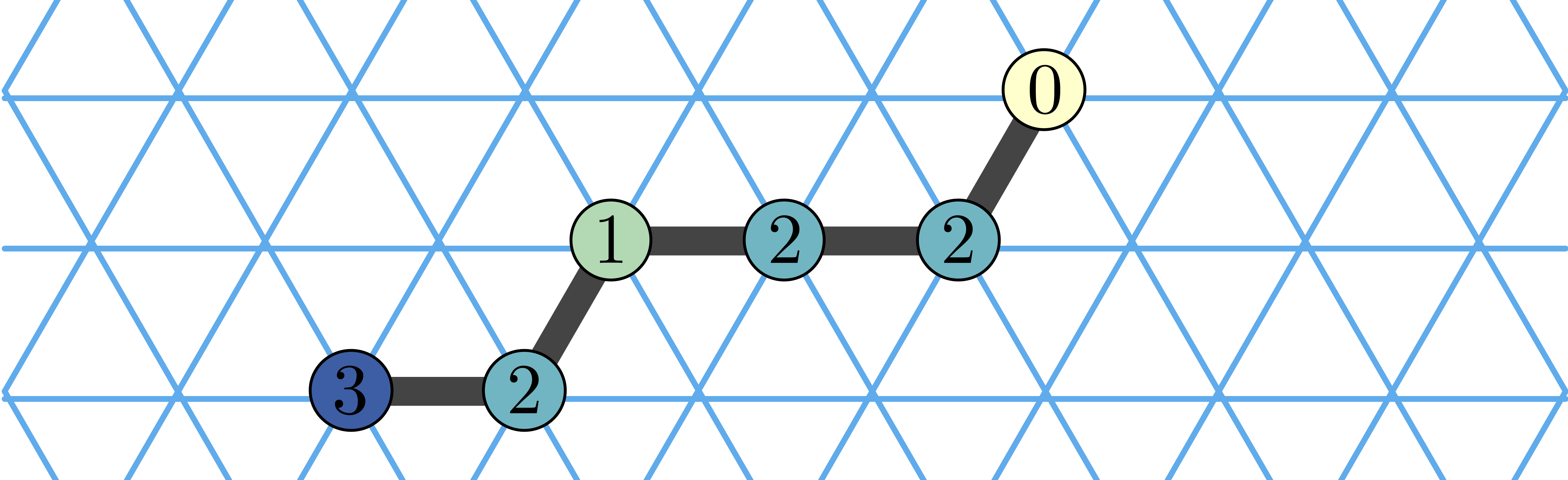
A trajectory, or computation, is a sequence of steps. At each step the move that happens is chosen uniformly at random.

We'd like to know what the model is capable of in general. For example, starting from a long line of monomers is it possible to have all trajectories fold into a Gosper curve?

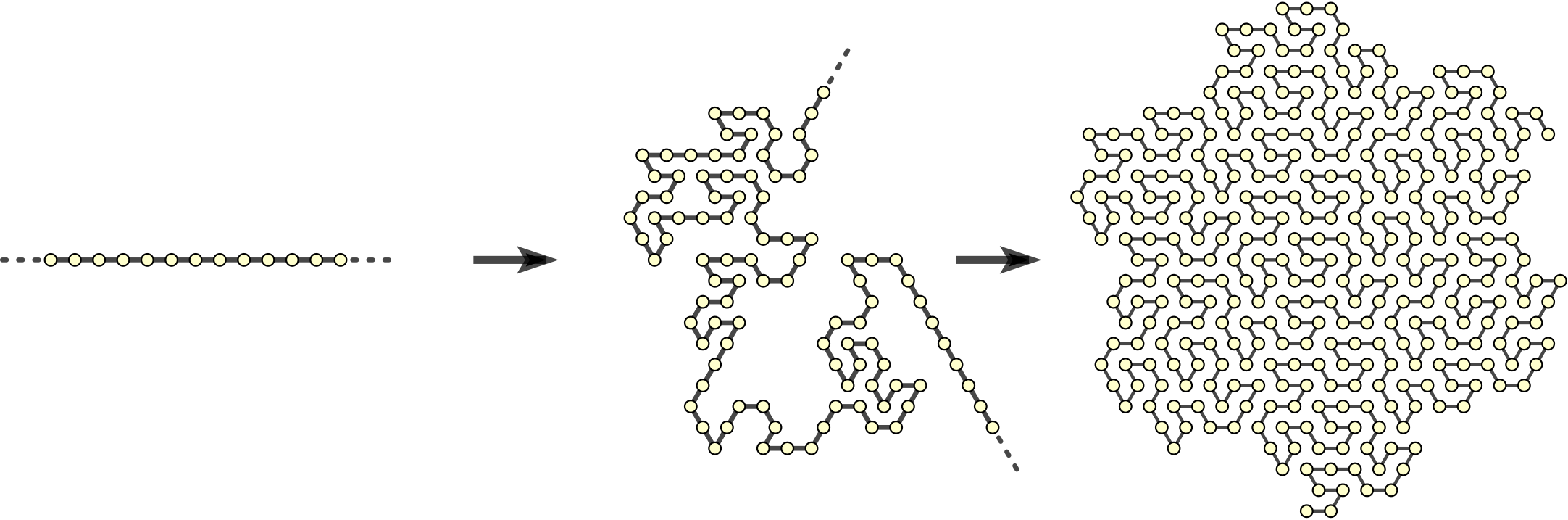
Actually, the answer to that question is no. When trying to fold that spiraly example some folding pathways might succeed, but some are permanently blocked--they get into an off-target locked arrangement where no further folding steps can happen. We already saw an example where it works, but here is one where it fails:

Result: line rotation

Luckily, we manage to show some positive results: shapes that can be folded and done so quickly.

The first key result, that surprised me, is that a line of monomer can be rotated by 5π/3, without getting permanently blocked on any trajectory.

First, here is an example of line rotation by π:

And now here is a full 5π/3 line rotation example:

The "program" embedded in the monomers is simple: each monomer begins in state 5, and the system just runs until all monomers have reached state 0. Plus its fast! O(log n) expected time to complete the rotation of a length n line. We show that that result is tight, by proving that rotation to 2π is impossible, meaning that any attempt to rotate by to 2π necessarily results in some permanently blocked trajectories.

Result: y-monotone shapes

By combining several line rotations, Turning Machines can fold squares laid out in a zig-zag raster pattern:

Although you see some blockings in the above video, we prove the are always temporary and are quickly "released", thus allowing the n x n square to fold in O(log n) time.

Other rastered shapes (called y-monotone shapes) can be similarly folded, here's an example such shape:

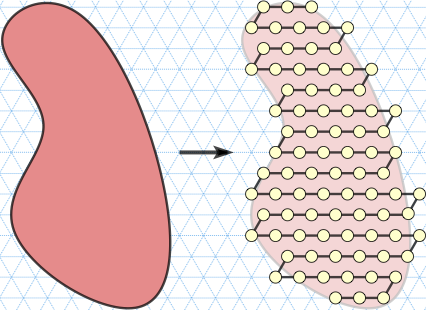
And here's another one being folded:

Our main result is that for any y-monotone shape with n points, there is a Turning Machine that on all trajectories folds the shape, and does so in merely O(log n) expected time.

While working with this model, the proofs turned out to be trickier than expected, and so our brains were indeed tested ... exactly what we wanted.