The 5th busy Beaver number is solved! BB(5) = 47,176,870. Congrats Tristan et al!
Today is a rare and amazing day!
Former group member, and current collaborator, Tristan, and his friends over on bbchallenge.org have settled the 5th Busy Beaver number, or BB(5), by finally announcing that they've proved BB(5) = 47,176,870. The work includes verifying the proof in the automated theorem-prover Coq, and now Tristan and co are diligently writing up this scientific tour-de-force for ultimate verification and community acceptance via beloved peer review.
Quanta magazine writer Ben Brubaker wrote a fantastic article on the 40-year history of this problem. I urge you to check it out! It gives background including fun anecdotes about the key characters over the past decades, up to and including Tristan's story about founding bbchallenge.org two years ago while he was a PhD student here at Maynooth. The collective at bbchallenge worked together to solve this monster problem, and any time I poked my head into their Discord server I could see they were having a lot of fun! Who wouldn't!
Here's a picture of the winning Busy Beaver Turing machine's execution, each line in the image corresponds to a step of the machine, starting at the top and ending at the bottom after 47,176,870 steps. The machine works in binary: 1s in white, 0s in black. You'd never guess from this image that it halts!
 All 47,176,870 steps of the BB(5) champion. Image posted on Discord by mxdys, a key player in bbchallenge who pioneered the Coq verification.
All 47,176,870 steps of the BB(5) champion. Image posted on Discord by mxdys, a key player in bbchallenge who pioneered the Coq verification.
I should add that I really enjoyed talking to Ben Brubaker from quanta. I have a lot of respect for a journalist that really wants to get to the bottom of why things work by asking me to prove non-trivial mathematical statements in my interview with him--it really felt like a scientific conversation. Science journalism needs more people like him, that understand the technical stuff, a thing of beauty for scientists, but yet can convey those ideas to a wide audience.
 BB(5) on the quanta magazine front page, with cool artwork.
BB(5) on the quanta magazine front page, with cool artwork.
What's a busy beaver?
Usually we write computer programs to do specific tasks. But theorists ask questions like: what can programs do in general? One of the creators of computer science, Alan Turing, thought in this way. He showed that there are programs capable of arbitrary algorithmic behaviour (universal programs, like your laptop's operating system that can run any other program), and that there are even problems that no computer program can solve.
A slightly crazy way to think about computing in general, not just programs we write day-to-day, is to consider all programs, not only the nice structured ones we tend to write. To do that, one should first pick a programming language. I pick Turning Machines. Then, let's cut down the infinite search space to a finite set, by putting a limit on program size. It turns out that even some tiny Turing Machines are already maximally complicated, called universal, meaning they can take any other program as input and run it, just like your laptop does. If you care, Turlough and I have a survey on small universal Turing machines and other 'small yet complex' models of computation.
But what if we further cripple machines by disallowing input? In the n-state busy beaver problem, we ask: for all of the n-state, 2-symbol Turing Machines, without input, which one halts in the longest number of steps? That machine would be called the n-state busy beaver, and the number of steps it takes before halting is BB(n). Machine that never halt don't count. It is known that: BB(1) = 1 and BB(2) = 6, [Rado, 1962], BB(3) = 21, [Rado and Lin, 1963], and BB(4) = 107, [Brady, 1983]. But, until today, 41 years later, BB(5) was unknown. For BB(5) Marxen and Buntrock [1990] showed that there is 5-state, 2-symbol machine that halts in 47,176,870 steps. Today's announcement is that Marxen and Buntrock's machine is the 5-state Busy Beaver! Out of the roughly 120 million other interesting machines (ignoring many symmetries) THAT machine takes the most steps before halting. Here's a picture of the first 1000 steps from bbchallenge:
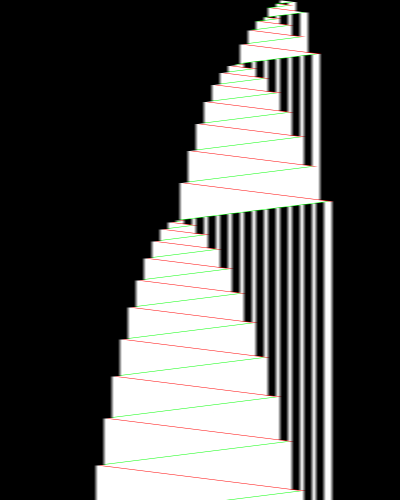 First 1000 steps of the BB(5) champion, generated by bbchallenge. Tape head movement is shown as green for Left, red for Right.
First 1000 steps of the BB(5) champion, generated by bbchallenge. Tape head movement is shown as green for Left, red for Right.
How was this finally proven? During his PhD, Tristan got a bee on his bonnet about BB(5), joking calling it the "simplest open problem in mathematics" since it is certainly simpler than BB(6), and BB(7), and and BB(8) and ... well, you know. Solving this problem would involve finding proofs of non-halting for millions of Turing machines (he figured around 120 million if we ignore certain symmetries). In a stroke of genius, Tristan decided to set up bbchallenge to crowdsource the problem! I watched, from afar, as more and more progress was made. But when I heard the rumblings recently that the end was in sight, I was really quite shocked at the speed this problem was resolved. Tristan's collective was only 2 years old, yet it's 41 year-old problem was slain! It really seems like the catalysis of bbchallenge.org made a difference, and I'm curious to see where this kind of "collaborative research ecosystem" can go in future.
The quanta article gives a better account of the history than I could possibly do, so check it out for more details. See also Scott Aaronson's blog post, and of course the bbchallenge announcement.
What's next?
There are tons of cool problems on simple-to-define models of computation that could be slayed with the collaborative bbchallenge-style approach. Can we answer questions about small universal Turing machines, such as finding the smallest machines for a given class of machines? Or showing that there are no such machines?
As mentioned in an earlier blog post, Tristan and I worked on the other direction, showing that BB(15) is at least as hard as solving a perhaps notorious open problem by Erdos. So somewhere between BB(6) and BB(15) lies the boundary of what we can prove with current mathematical technology. How far can we push these bounds in either direction? That's the next big unknown.
 The challenges keep coming! Screenshot of bbchallange.org on 2024-7-2.
The challenges keep coming! Screenshot of bbchallange.org on 2024-7-2.