Computing with small tile sets — new paper at DNA27
We have a new paper, written with Matthew Cook, investigating universal computation using small tile sets, published at DNA27.
Computing with square tiles in the plane is an idea that seems to have emerged soon after the introduction of Hao Wang's 1961 tile-based model (see the original paper), for instance in Robert Berger's 1966 result on the "undecidability of the domino problem" (more on that topic). Then, in 1998, Erik Winfree introduced the abstract Tile Assembly Model (aTAM) in his PhD thesis. This model, due to its simple yet powerful formalism, and the fact it is implementable in the wet-lab using DNA tiles, has been of great influence to the fields of algorithmic self-assembly and molecular computing. In the aTAM, a programmer designs tile sets that asynchronously assemble a target structure (for instance a shape or the result of a computation) starting from a seed which is generally comprised of one tile or a connected assembly of tiles.
A legitimate question that arises from studying the aTAM is: how small can a tile set be and yet provide interesting behavior? By interesting, we mean, for instance, the ability to compute any Boolean function that would be encoded in an appropriate seed.
In our new paper, we attempt to answer that question by first slightly modifying the aTAM so that growth starts from a new type of seed, one that is disconnected. Here's one example of such a disconnected seed that looks a bit like a maze:

Example of a disconnected seed. Here two glues are used to encode information: '0' and '1', along with a special glue 'null' glue (dark grey). All the tiles (and glues) of this seed are constant except for the circled ones which specify the system's input, here: '110'.
We call this model the Maze-Walking TAM as disconnected seeds resemble mazes that tiles may flow through. Note that the idea of having disconnected seeds can seem odd at first: the whole point of the aTAM is to model interactions between free-floating molecules, and it may not be obivious how free-floating 2D disconnected seeds could ever spatially arrange in the exact way we need them to. However, the idea becomes less weird if we assume that all disconnected components are attached to the same underlying surface, for instance a DNA Origami. This way of thinking also relates to an existing trend in the DNA computing literature of computing on a surface, see Section 2.2 of our paper.
In the Maze-Walking TAM, we exhibit a tile set with 4 tiles that we call the NAND-NXOR tile set, and a tile set with 6 tiles that we call the Collatz tile set, that are each able to run any Boolean circuit:
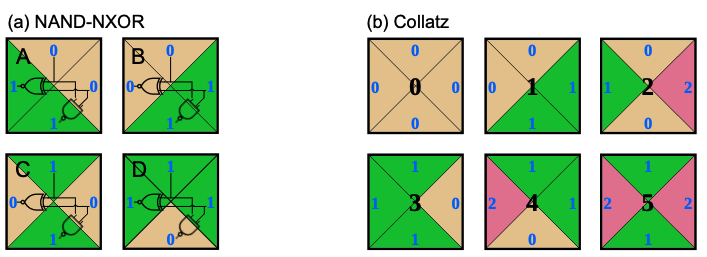
The NAND-NXOR tile set and the Collatz tile set.
In our results, disconnected seeds encode Boolean circuits, and our two small tile sets give the elementary computing power to run those circuits by flowing information (tiles) through the encoded circuit. Here is an example run with the NAND-NXOR tile set starting from the same seed as above:
The process of tile-assembly in the Maze-Walking TAM with the NAND-NXOR tile set starting from the disconnected seed shown previously. Tiles attach asynchronously to the structure until it is completed.
In our paper we only studied systems such as the above one where the growth is directed, i.e. there is only one tile that can possibly attach at any position of the final structure.
The disconnected seed shown above actually encodes a Boolean circuit that recognises three-bit prime numbers! Here the input is '110', the number 6 in binary, which is not prime. Hence, the output is '0', which is displayed bottom-left (as the southern glue of the south-western most tile of the assembly):
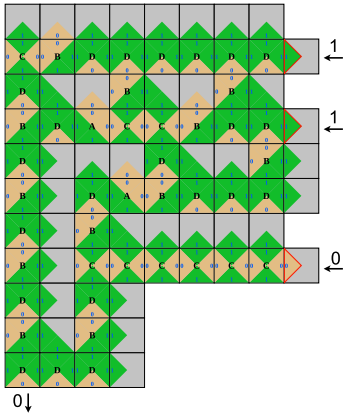
Result of the computation specified by the prime-recognition disconnected seed, the NAND-NXOR tile set, and the input tiles '110': the number 6 (110 in binary) is not prime.
For an input that is prime, such as '111' (the number 7 written in binary), the output is '1' as shown in the last frame of this movie (look at the south glue of the south-western most tile):
Running the Maze-Walking TAM with the NAND-NXOR tile set on the prime-recognition seed with input '111' (the number 7) that is prime.
The NAND-NXOR tile set was constructed by hand and used for its intrinsic abilities to produce logic gates "NAND" and "NXOR" which can be used to implement all the gadgets needed to run any Boolean circuits: crossover gates (simulating the crossing of two wires) and all 2-input 1-output logic gates (OR, AND, XOR, etc...).
However, the six-tiles Collatz tile set was found "in nature" by Matthew Cook. The tile set has three glues '0', '1' and '2'. This tile set appears naturally when studying the relationship between base 2 encodings and base 3 encodings and is intrinsically able to compute some arithmetic primitives such as Euclidean division by 2n or 3n solving the Chinese Remainder Theorem in Z/2nZ x Z/3mZ.
With the help of two extra tiles, it can also be used to simulate the Collatz process, hence its name. Indeed, with the help of two extra tiles, any binary input of size n can be used to assemble the n first iterations of the Collatz process: the output will be read in ternary. This result is intimately related to our previous paper on base conversion in the Collatz process. Here's an example:
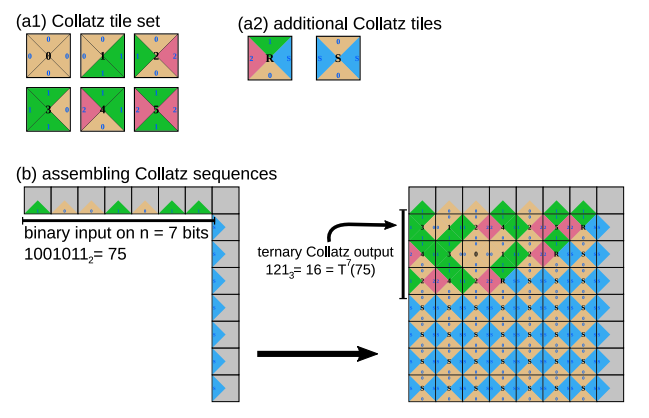
(a) The Collatz tile set (b) Two additional tiles required to run Collatz sequences (b) The Collatz tile set assembles Collatz sequences in the Maze-Walking TAM. The binary input of size n is given in binary on the North side of a n by n square. The East side of the square is constant and only advertises glue 'S'. After assembling, the nth Collatz iterate of the input is represented in ternary on the West side of the square.
In the context of the Maze-Walking TAM, the Collatz tile set is able, like the NAND-NXOR tile set, to run any Boolean circuit (see Section 5 of our paper). Circuit gadgets (crossover and logic gates) were found by computer search (as opposed to being designed by hand) and rely on the ability of the Collatz tile set to generate complex (one might even say "chaotic") patterns. This result opens the road for future work to look at Collatz sequences themselves in order to see if they embed such circuit gadgets naturally, which in turn would help to characterise the as-yet-unknown computational power of the Collatz process.
The Collatz tile set can also be used to compute powers of two in base 3 which is the subject of an open question by Erdős [1979]: "for all n>8 there is at least one digit 2 in the base 3 representation of 2n". This is the subject of our paper on the hardness of knowing busy beaver values BB(15) and BB(5,4).
Finally, our study of the Maze-Walking TAM leaves some questions open, such as:
- Can Boolean circuit simulation, or any kind of universal computation, be achieved in the Maze-Walking TAM using tile sets with less than 4 tiles? I.e. Can we beat the NAND-NXOR tile set in terms of how many tiles are needed to simulate any Boolean circuit?
- Can interesting behaviour occur in the Maze-Walking TAM with just 1 tile? (At first sight, this question may look odd, however one could imagine encoding a bit by the absence or presence of a tile at a given position in the final assembly, leaving room for expressiveness in the Maze-Walking TAM with 1 tile.)
- Is the Maze-Walking TAM, with ≤ 4 tiles, intrinsically universal for the aTAM?
A simulator was built to study the Maze-Walking TAM, it is open source and can be found at this address: https://github.com/tcosmo/mawatam.